La cryptographie décryptée pour une utilisation simple et pratique.

Depuis "l'arrivée d'Internet dans tous les foyers", les échanges d'informations sont grandement facilités. Reste qu'avec ce flux d'informations permanent, on peine à trouver un espace de confidentialité. La cryptographie, vielle de plus de 3000 ans, apporte une solution à la sécurisation des informations confidentielles et personnelles. Nous allons voir d'où elle tire ses origines, comment cela fonctionne-t-il et surtout comment l'utiliser simplement au quotidien.

Historique de la cryptographie

La cryptographie remonte à l'antiquité, le premier "document" crypté connu est une tablette d'argile découverte en Irak qui date du 16ème siècle avant JC. Un potier y avait gravé sa recette secrète en supprimant des consonnes et en modifiant l'orthographe des mots. Il faut attendre la Grèce antique (200 ans avant JC) pour voir apparaître le premier vrai système de cryptographie: le carré de Polybe. Ce système quand on le regarde aujourd'hui ressemble plus aux jeux que l'on trouve dans les cahiers de devoirs de vacances pour enfants. Le principe consiste à remplacer une lettre par sa coordonnées dans un carré de 5x5 (cf: image).

De Jules César aux débuts du siècle, de nombreux politiques et scientifiques se sont essayés à la cryptographie, sans grand succès il faut le dire. On peut noter la tentative de Jules César dans ce domaine, son idée consistait tout simplement à décaler de trois rangs dans l'alphabet les lettres d'un message et de supprimer les espaces et à le redécouper aléatoirement ("la vie est belle" devenait "odyl hh vweho oh").

Blaise de Vigénère (1523 - 1596) est un des premiers à inventer un système à faire intervenir un mot de passe pour chiffrer le message. La méthode de Blaise de Vigénère est basée sur un carré de 26x26 dont chaque case comprend une des lettres de l'alphabet. Le texte codé s'obtient en prenant lettre à lettre, l'intersection de la ligne qui commence par la lettre à coder avec la colonne qui commence par la première lettre du mot de passe. Pour la deuxième lettre à coder, on utilise la deuxième lettre du mot de passe et ainsi de suite. Dès que l'on atteint la fin du mot de passe, on recommence à la première lettre. Sur l'image ci-contre, avec comme mot de passe "karting", la lettre "M" devient "W" après avoir été codée.

Excepté les défis actuels concernant la cryptographie, c'est certainement la machine "Enigma", conçue par les Hollandais et utilisée par les allemands pendant la guerre qui a suscité le plus de recherches et d'interrogations au sein du milieu scientifique. Son secret fut finalement découvert par des mathématiciens anglais. La mécanique de "Enigma" était basée sur deux Claviers l'un servant à saisir le texte en clair et l'autre à afficher le texte codée en éclairant la lettre correspondante. Utilisé à l'envers (le clavier "codé" pour la saisie), il permettait de retrouver le texte initial.
Le mécanisme était un savant mélange de cryptographie et de mécanique : plusieurs rotors comprenant toutes les lettres de l'alphabet dans un ordre différent étaient combinés pour donner la lettre chiffrée. La force de "Enigma" provenait d'une part du fait qu'à chaque codage, les rotors étaient décalés ce qui ne permettait par de retrouver la clé en recherchant des répétitions de lettres. La clé de chiffrage permettait de déterminer l'orientation initiale de chacun des rotors.

Ordinateurs, binaire et cryptographie

Avec l'arrivée des ordinateurs, le remplacement n'est plus le problème principal, aussi bien du côté de la personne qui chiffre que de celui de celle qui déchiffre. La formule de cryptage est simplement modélisée par une formule mathématique plus ou moins complexe qu'il suffit d'appliquer en lui combinant la clé pour obtenir le message en clair.
Pour créer un formule de cryptage, il suffit " simplement " que celle-ci soit réversible, c'est à dire qu'en l'appliquant à l'envers en lui combinant la clé, on retrouve les informations de départ.

En informatique, les caractères alphanumériques étant stockés sous la forme d'une valeur ASCII (comprise en 0 et 255). Une des formules les plus utilisées pour encoder des mots de passe dans des logiciels grands public, consiste à appliquer un "OU exclusif" (XOR en abrégé) entre le texte à coder et la clé. Le " OU exclusif " est une fonction binaire, donc très simple et très rapide à mettre en œuvre en informatique, qui ne retourne la valeur 1 que si les deux bits comparés sont différents. C'est le " OU " de l'expression " fromage OU dessert " : l'un ou l'autre, mais pas les deux. La table de vérité qui décrit le fonctionnement du " OU exclusif " ce trouve ci-dessous :


Pour utiliser cet algorithme, il suffit de remplacer le texte à chiffrer et le clé par leur équivalent ASCII de d'appliquer la fonction XOR entre le premier caractère du texte à chiffrer et le premier caractère de la clé, le deuxième caractère du texte à chiffrer et le deuxième caractère de la clé, ainsi de suite. Lorsqu'on arrive en fin de clé, on reprend au début.
La méthode " OU exclusif " est simple à décrypter en utilisant le moyens informatiques actuels, c'est pourquoi elle n'est utilisé que pour protéger des informations peu sensibles (mot de passe de l'économiseur d'écran Windows par exemple).

Le chiffrement DES (Data Encryption Standard), plus complexe et inventé par dans les années 60, est une succession de permutations, de décalages et de fonctions mathématiques, toutes réversibles. La seule manière de décrypter cet algorithme, et tous ceux basés sur des fonctions mathématiques réversibles, consiste à utiliser la force brute pour retrouver la clé. Plus la clé est longue (codée sur un nombre élevé de bits), plus il va falloir de temps pour essayer toutes les possibilités. DES utilise une clé de chiffrement de 64 bits ce qui donne 2 puissance 64 possibilités à essayer.

A l'heure du e-commerce, c'est l'algorythme RSA 512 ou 1024 bits qui est le plus utilisé aujourd'hui à chaque fois qu'une transaction sécurisée s'effectue entre votre ordinateur et une banque lors d'un paiement en ligne (l'adresse qui apparaît dans le navigateur commence par https://). Il faut environ 107 millions d'années à un Athlon 1Ghz pour retrouver par la force brute une clé codée sur cette longueur.

On peut considérer qu'une clé RSA 512 bits peut aujourd'hui être cassée en utilisant des moyens de calculs distribués : plusieurs centaines d'ordinateurs recherchent en parallèle la même clé, mais ces moyens sont hors de portée d'un particulier. Par contre, une clé sur 1024 bits, qui N'EST PAS deux fois plus difficile à casser mais 1,3x10 puissance 154 fois plus compliquée à casser (chaque bit supplémentaire multipliant par deux le nombre de clé possibles) peut être considérée à l'heure de cet article comme complètement indéchiffrable. Il paraît probable que dans les années à venir, les progrès des mathématiques et de l'informatique combinés permettrons d'arriver à bout d'un telle clé.

On peut donc considérer que le RSA 1024 bits est sûr à 100%…. à l'heure actuelle.

La cryptographie au quotidien : PGP

Sans être un maniaque de la cryptographie, celle-ci peut être utilisée au quotidien pour plusieurs raisons. La première résulte de la généralisation des "trojans" qui permettent à des personnes mal intentionnées de pénétrer sur une machine infestée. On a tous des informations stockées sur nos Disques durs que l'on préfèrerait éviter de divulguer (mot de passe de sites Web, numéros de série de shareware enregistrés, liste de clients, ...).

Pour utiliser la cryptographie au quotidien, il faut parvenir à trouver un juste compromis entre sécurité et simplicité d'utilisation. De nombreux logiciels de cryptographie existent et peut être qu'une simple protection par fichier .zip avec mot de passe suffira à vos besoins. Pour y répondre, il faut se poser les questions suivantes:

- Quelle est l'importance de mes données confidentielles : si vous souhaitez protéger un secret d'état, vous préfèrerez utiliser les derniers algorithmes quitte à ce que la procédure pour crypter et décrypter les données soit lente et peu pratique. Si vous souhaitez simplement stocker des mots de passe de connexion Internet ou d'accès à des comptes sur des sites Web, peut être que de les stocker dans un fichier texte compressé au format .zip avec mot de passe suffira. Peut être encore suffira-t-il de les noter sur une feuille de papier que vous rangerez dans le tiroir de votre bureau (pourquoi faire simple... quand on peut faire compliqué).

-Qui est susceptible d'être intéressé par ces données confidentielles : si vos données permettent d'escroquer de l'argent (numéro de carte bleu, mot de passe d'accès à un site de banque...), les personnes qui les interceptent mettront plus d'énergie à tenter de les décrypter que s'il s'agit d'une lettre d'amour secrète que vous souhaitez éloigner des yeux de votre frère cadet !

- Quel est le risque si je perd le mot de passe : Ce point est très important, si vous perdez votre mot de passe, toutes les informations cryptées seront perdues à jamais. Il faut donc choisir un mot de passe " inoubliable " mais pas trop simple ou noter le mot de passe dans un endroit sur (on finit par tourner en rond).

Pour être efficace au quotidien, la cryptographie doit être simple d'utilisation et transparente au maximum pour l'utilisateur. Nous vous proposons dans le cadre de cet article l'utilisation de deux logiciels qui ont TRES LARGEMENT fait leurs preuves dans ces deux domaines: PGP (Pretty Good Privacy) et Scramdisk.

Utilisation pratique de PGP

PGP a été créé par Phil Zimmerman en 1991. Ce développeur avait souhaité à l'époque créer un logiciel qui apporte une "assez bonne intimité" (Pretty Good Privacy en anglais).

Le principe de PGP repose sur un système de double clé. Il existe une clé publique qui peut être librement diffusée et qui permet de chiffrer un message que seul le possesseur de la clé privée peu déchiffrer. Ce système permet de s'affranchir des risques liés au transfert du mot de passe de décryptage à son correspondant. En effet, avec les techniques de cryptage conventionnelles, comment transmettre le mot de passe de déchiffrage à un correspondant en étant sûr que celui-ci ne tombe pas entre les mains de quelqu'un d'autre ?

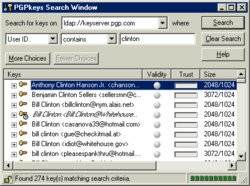
Avec PGP, le message que je souhaite envoyer est crypté avec la clé publique de mon correspondant. Cette clé peut être soit diffusée par mon correspondant, soit téléchargé sur Internet depuis un serveur de clés publiques. En aucune manière la clé publique ne permet de décrypter un message. Seul le possesseur de la clé privée correspondant à cette clé publique pourra décrypter le message. La clé privée permet également de signer un message, garantissant sans équivoque l'origine d'un message.

La première installation de PGP se termine par la création d'un lot de clés. Ce lot contient la version publique et la version privée de votre trousseau de clé. La clé privée s'utilise conjointement à une "passphrase" (phrase cachée). La "passphrase" pour être réellement efficace doit être mémorisée. La meilleurs méthode pour construire une "passphrase" consiste à créer une phrase longue mais simple combinant chiffres, lettres et si possibles caractères divers (ex: "1 tient vaut mieux que 2 tu l'auras" ou "j'M les pommes & les pêches").

Autant la clé publique peut être largement diffusée à vos correspondant sans craintes, autant la clé privée doit être stockée à l'abri et sauvegardée (sur disquette ou CD-Rom). Sans clé privée, il est IMPOSSIBLE, même avec la passphrase de déchiffrer un message.

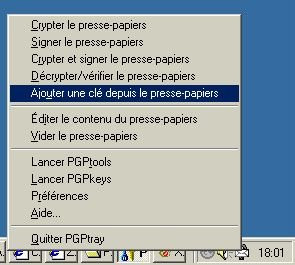
PGP se loge dans la barre des tâches et permet de crypter le presse-papier Windows. Pour crypter un message, il suffit donc de faire un copier du texte en question et de sélectionner "Crypter le presse papier" après avoir cliqué avec le bouton droit sur l'icône PGP dans la barre des tâches. Sélectionnez la clé publique de votre correspondant et faites la glisser dans la liste des destinataires. Pour finir, il ne reste plus qu'à "coller" dans votre document pour voir apparaitre une série de caractères commençant et terminant par les lignes suivantes:

Votre correspondant, pour déchiffrer le message, n'aura qu'à copier le bloc de texte délimité par les deux lignes précédentes, sélectionner l'option "décrypter le presse-papier", saisir sa "passphrase" pour voir apparaître le message en clair.

PGP contient un gestionnaire de clés qui permet de stocker les clés publiques de ses correspondants et de trouver la clé publique d'un correspondant à partir de son nom ou de son adresse email. Cette fonction est disponible grâce aux nombreux serveurs de clé publiques qui sont disponibles autour de la planète et qui enregistrent après chaque création de clé la définition de celle-ci.

Plusieurs versions de PGP existent et contrairement à la coutume en informatique, il n'est pas ici nécessaire d'installer la dernière version. La version 5.5.3 française qui a fait ses preuves est légère à télécharger et permet de décrypter les message cryptés avec une version plus ancienne. La dernière version apporte tout de même la possibilité intéressante de pouvoir crypter à la volée une conversation ICQ entre deux utilisateurs de PGP (garantissant la confidentialité de l'échange contre une interception de paquets d'informations par un pirate).

Les conseils:
- Ne communiquez ni n'écrivez JAMAIS votre "passphrase"
- Même si sans la "passphrase", la clé privée est de peu d'utilité, il vaut tout de même mieux stocker la clé privée dans un lieu sur (CD-Rom, disquette)
- Pour que la cryptographie soit réellement efficace, il faut qu'elle soit utilisée à bon escient. Ne cryptez pas un message qui n'a rien de confidentiel, cela ne servirait qu'à énerver votre correspondant.

Utilisation pratique de Scramdisk

Scamdisk s'oriente plus vers la sécurisation des données confidentielles contenues sur le disque dur que vers l'échange sécurisé, comme ça pourrait l'être avec PGP. Il permet de créer une partition Windows, qui s'utilise comme n'importe quel disque dur, mais qui possède la particularité d'être complètement cryptée: tous les fichiers qui y seront copiés seront cryptés à la volée.

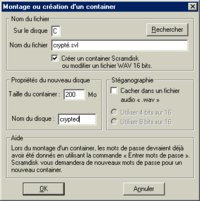
Le principe repose sur la création d'un "fichier container" qui contient toutes les informations de la partition. Au démarrage du logiciel (ou au lancement de Windows), le fichier container est "monté" c'est à dire qu'il devient une partition à part entière. Lorsqu'on quitte Windows, ou bien lorsqu'on arrête le logiciel, le fichier container doit être "démonté".

Cette méthode présente plusieurs avantages:
- Dès que la partition cryptée est montée, le cryptage des informations se fait à la volée et la partition s'utilise comme n'importe quelle autre partition Windows.
- Lorsque le volume est démonté, toutes les informations sont stockées dans un seul et unique fichier container qu'il est simple de sauvegarder ou de transmettre à un correspondant.

L'utilisation de Scramdisk est simple dès que l'étape de création du container est terminée. Au premier lancement de Scramdisk, un fenêtre vous demande (bizarrement) une série de mots de passe. Annulez et ouvrez le menu /fichier/Monter-Créer un nouveau volume. Dans la fenêtre qui suit, il suffit d'indiquer le disque sur lequel sera stocké le container (C: par défaut), de donner un nom au fichier (extension .svl) et de cocher la case "Créer un container Scramdisk" puis d'indiquer la taille et le nom du container. L'écran suivant permet de formater le container.
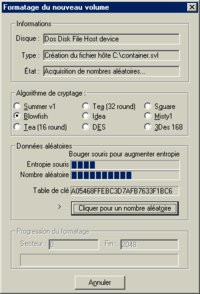
Choisissez l'algorithme de cryptage (l'algorithme Blowfish par défaut est un bon choix) et appuyez sur la touche entrée un grand nombre de fois afin de générer une série de chiffres aléatoires (qui sert de base au cryptage). Pour terminer, Scramdisk vous propose d'associer un ou plusieurs mots de passe à ce fichier container.

Lorsque le disque container est créé, il suffit de le monter en utilisant le même menu que celui utilisé pour créer un container ou bien tout simplement en glissant le fichier .svl sur l'interface du logiciel. Lorsque le container est monté, il apparaît dans l'explorateur Windows comme n'importe quel autre disque dur Windows.

Dès que le container monté est devenu inutile, il faut penser à le démonter. Si vous quittez Windows avec un disque Scramdisk monté, un écran bleu vous indiquera de le faire. Pour éviter ce problème, il suffit d'utiliser la commande de démontage automatique temporisé du menu "configuration". Celui-ci permet de démonter un container lorsqu'il n'a pas été utilisé pendant une période déterminée.

Un documentation complète en français de Scramdisk au format PDF (mais avec des copies d'écran en anglais) est téléchargeable sur ce lien.

Conclusion

Vous l'aurez compris, la cryptographie est un domaine extrêmement vaste. Cette petite introduction devrait permettre à n'importe qui d'y faire ses premiers pas et n'oubliez pas cette citation: